基于最小二乘法leastsq的双孔隙土水曲线拟合
2018-04-20
2018
模型内容:
Dexter AR, Czyż EA, Richard G, Reszkowska A. A user-friendly water retention function that takes account of the textural and structural pore spaces in soil. Geoderma. 2008;143(3):243-53.
基于Python编写了基于最小二乘法的双孔隙土水曲线拟合,记录在此,以便以后查阅。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | # -*- coding: utf-8 -*-
"""
Created on Thu Apr 19 22:40:35 2018
双孔隙土水曲线基于最小二乘法拟合
@author: Think
"""
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
#from data import x,y #从外部导入想要拟合的数据,h,theta都是ndarry类型的数据
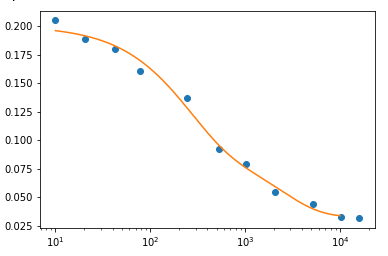
h=np.array([9.9, 20.5, 42.4,78.47,245.18,526.86,1010,2056,5227,10234,16000])
theta=np.array([0.2051,0.18916,0.18,0.1605,0.1368,0.092,0.079,0.05481,0.04437,0.03278,0.03171])
def fun(p, h):
"""
定义想要拟合的函数
"""
c1,A1,h1,A2,h2 = p #从参数p获得拟合的参数
return c1+A1*np.exp(-h/h1)+A2*np.exp(-h/h2)
def err(p, h, theta):
"""
定义误差函数
"""
return fun(p,h) -theta
#定义初始值
p0 = [0.3,0.233,1000,0.1,100]
xishu = leastsq(err, p0, args=(h,theta))
c1=xishu[0][0]
A1=xishu[0][1]
h1=xishu[0][2]
A2=xishu[0][3]
h2=xishu[0][4]
print (xishu[0])
# xishu[0],即为获得的参数
plt.semilogx(h,theta,'o')
h=np.logspace(1,4,1000)
#plt.plot(np.log10(h),c1+A1*np.exp(-h/h1)+A2*np.exp(-h/h2))
plt.semilogx(h,c1+A1*np.exp(-h/h1)+A2*np.exp(-h/h2))
|
最后图形
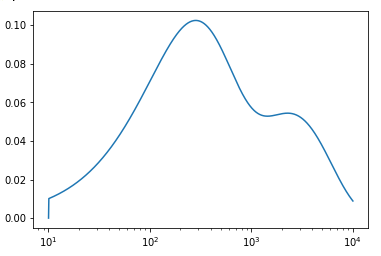
第二步:求解孔隙分布,即dw/d(logh)
本来想用Sympy符号运算的,但是出现log10,微分出现问题,直接采用最原始的手动微分。
1 2 3 4 5 6 7 8 9 10 | #from sympy import *
import numpy as np
import matplotlib.pyplot as plt
#手动计算导数
k=np.linspace(0,0,999)
h=np.logspace(1,4,1000)
for i in range(1,999):
k[i]=-(fun(xishu[0],h[i])-fun(xishu[0],h[i-1]))/(np.log10(h[i])-np.log10(h[i-1]))
plt.semilogx(h[1:],k)
|
Comments