基于Berkeley Madonna进行常微分方程拟合

基于Matlab Optibox工具箱进行常微分方程参数拟合
之前师姐需要拟合动力学方程，让我帮她参考下，我查找了下Berkeley Madonna的教程，整理记录了下，便于以后使用。
需要的方程如下:

1
2
3
4
5
6

dx(1)=0;
dx(2)= k(1)*x(1) – k(2)*x(2) – k(3)*x(5) + k(4)*x(6);
dx(3)=0;
dx(4) = -k(2)*x(3)*x(4) + k(3)*x(5);
dx(5) = k(8)*x(3)*x(4) – k(7)*x(5) – k(3)*x(2)*x(5) + k(5)*x(6);
dx(6) = k(6)*x(2)*x(5) – k(3)*x(6) – k(4)*x(2)*x(6);

本文首先讲述的是使用Berkeley Madonna程序进行拟合计算。
程序下载链接

程序使用

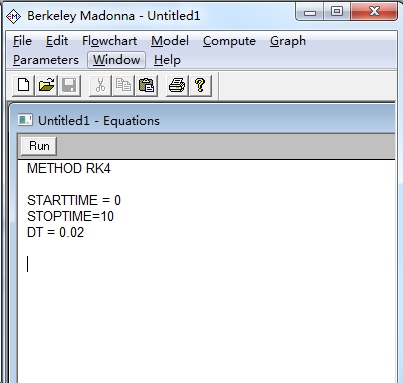
程序主界面：

程序的编写如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

METHOD RK4
STARTTIME = 0
STOPTIME = 90
DT = 0.02
d/dt (A) =+k9*D+k8*C
d/dt (B) =-k1*B-k7*B+k2*D+k4*C
d/dt (C) =-k4*C-k8*C-k2*C++k5*D
d/dt (D) =-k2*D-k9*D-k5*D+k1*C
init A =0
init B = 20
init C = 0
init D = 0
k1=0.2
k2=0.2
k3=0.2
k4=0.2
k5=0.2
k6=0.2
k7=0.2
k8=0.2
k9=0.2

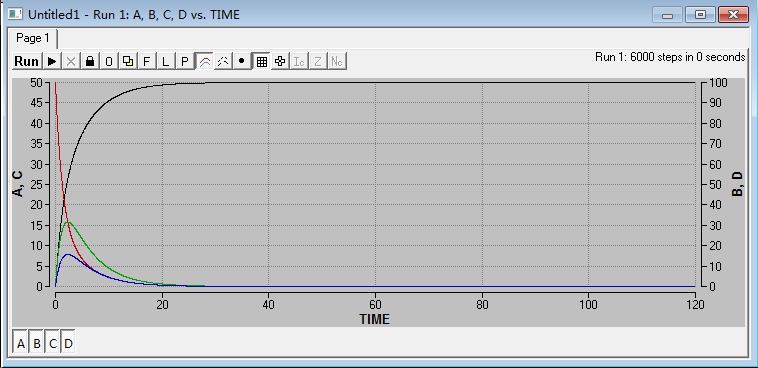
主程序比较简单，d/dt(a)=…是微分方程组，initA 是组分A的初始值，k1=0.2是所求参数的初始值。运行run即可以得到四种组分随时间的变化曲线。

得到ABCD四种材料随时间的变化。

参数拟合

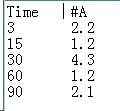
将ABCD四种材料是量随时间的变化编制成txt文件，如下图

导入：

File-import dataset
拟合：
Parameters-curve fitting

双击k1 k2..导入进Parameters.
点选MultipleＦ　将Fit　Variable 与 To dataset对应 ，点击Add.
最后点选OK。

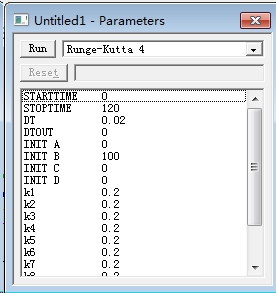
结果

点选 Parameter-Parameters windows.如下图

拟合后的k.