有限差分法-热传导方程-显式法
2017-07-03
2017
整理了下有限差分法,为大变形固结有限差分的计算准备下。
热传导方程如下:
初始条件:
T=sin函数
边界条件:
左边界:0
右边界:0
长度1,
时间1,
传导系数1/4
Matlab程序
%%sd
% Explicit Method
clear;
% Parameters to define the heat equation and the range in space and time
L = 1.; % Length of the wire
T =1.; % Final time
% Parameters needed to solve the equation within the explicit method
maxk = 2500; % Number of time steps
dt = T/maxk;
n = 50; % Number of space steps
dx = L/n;
cond = 1/4; % Conductivity
b = cond*dt/(dx*dx); % Stability parameter (b=<1)
% Initial temperature of the wire: a sinus.
for i = 1:n+1
x(i) =(i-1)*dx;
u(i,1) =sin(pi*x(i));
end
% Temperature at the boundary (T=0)
for k=1:maxk+1
u(1,k) = 0.;
u(n+1,k) = 0.;
time(k) = (k-1)*dt;
end
% Implementation of the explicit method
for k=1:maxk % Time Loop
for i=2:n; % Space Loop
u(i,k+1) =b*u(i+1,k)+(1-2*b)*u(i,k)+b*u(i-1,k);
% u(i,k) + 0.5*b*(u(i-1,k)+u(i+1,k)-2.*u(i,k));
end
end
% Graphical representation of the temperature at different selected times
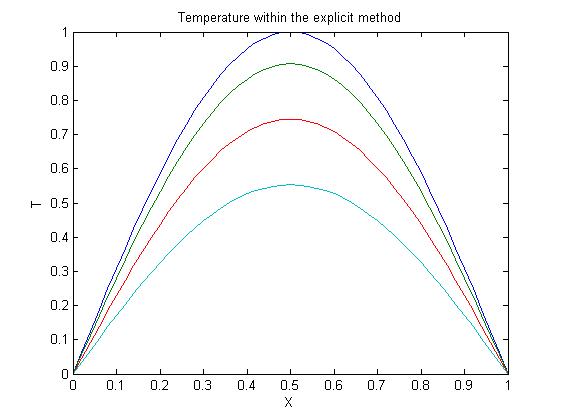
figure(1)
plot(x,u(:,1),'-',x,u(:,100),'-',x,u(:,300),'-',x,u(:,600),'-')
title('Temperature within the explicit method')
xlabel('X')
ylabel('T')
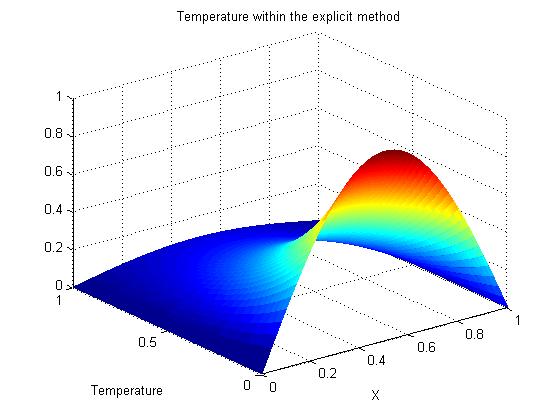
figure(2)
mesh(x,time,u')
title('Temperature within the explicit method')
xlabel('X')
ylabel('Temperature')
结果:
Comments